Common Core Math Examples: CCSS Math Samples for All Ages
/If your child attends public school in the United States, you’ve most likely encountered the baffling “new math” known as Common Core.
In reality, Common Core math is not as complex as it may appear on the surface. In fact, students are still learning traditional math skills. The difference is that students are now learning additional methods that teach them “Number Sense,” or an understanding of how and why math problems really work.
Still, Common Core math can be strange and confusing at first. To help unravel some of the mystery, we’re providing Common Core math examples for every grade level, as well as an explanation of CCSS Mathematics standards. Let’s get started!
What is Common Core?
First of all, what exactly is Common Core, and why is it such a huge topic in education?
Simply put, the Common Core State Standards (CCSS) is a list of skills and knowledge students should master in English Language Arts and Mathematics at each grade level. By gradually acquiring these skills, students should be prepared for college or a career by the time they graduate high school.
The push for a set of common national standards began in 2007, largely based on fears that the United States was falling behind other countries academically. The goal was to create a rigorous set of shared standards in English Language Arts and Mathematics to promote college and career readiness.
At a 2009 summit in Chicago, the National Governors Association and the Council of Chief State School Officers led the initiative to build state support. The standards were drafted by work groups consisting of K-12 teachers, university professors, experts from testing companies, and leaders of education advocacy groups.
In 2010 and 2011, all but four states adopted the Common Core State Standards.
The reaction to Common Core has been mixed. Several states have since backed out of their agreement to implement Common Core, and even more states have reversed their decision to administer tests designed to measure mastery of CCSS.
However, CCSS is still used in forty-two states, with the national exceptions being:
CCSS is also implemented in the District of Columbia, and many of the states that have dropped the Common Core name still utilize standards that are very similar to CCSS.
Common Core Math: Examples and Standards
Common Core math skills are organized into the following domains:
In the following sections, we’ll take a closer look at each domain, including Common Core math examples and a description of the skills students at each grade level must demonstrate to show mastery.
Counting and Cardinality (K)
Kindergarten students should know number names and the count sequence. They should also be able to count objects and compare numbers.
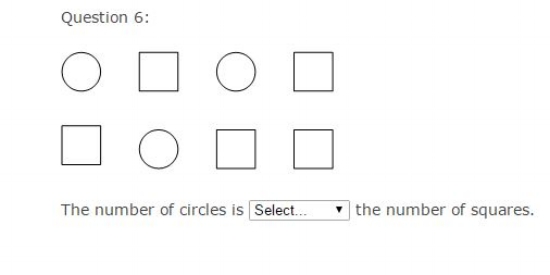
For example, students should be able to identify whether the number of objects in a group is greater than, less than, or equal to the number of objects in another group.
Common Core Math Examples - Counting and Cardinality Sample Question
Operations and Algebraic Thinking (K-5)
To demonstrate this skill, kindergarten students should understand that addition means putting together and adding to, and that subtraction is taking apart and taking from. They should also be able to fluently add and subtract within 5.
First grade students are expected to demonstrate the following skills:
At the second grade level, students must demonstrate the same skills as first grade students. In addition, they must also work with equal groups of objects to gain foundations for multiplication.
For example, they should be able to determine whether a group of objects (as many as 20) has an odd or even number by pairing objects or counting them by 2s.
Third grade students should be able to:
Common Core Math Examples - Operations and Algebraic Thinking Sample Question
Fourth grade students are asked to use the four operations to solve problems, gain familiarity with factors and multiples, and generate and analyze patterns.
For example, given the rule “Add 3” and the starting number 1, fourth grade students should be able to generate a list of numbers in the sequence. They should then observe that the numbers alternate between odd and even numbers and should be able to explain why this is so.
Lastly, fifth grade students are expected to write and interpret numerical expressions and analyze patterns and relationships.
Number and Operations in Base 10 (K-5)
This domain is focused on understanding the concept of place value.
Kindergarten students build the foundation for understanding place value by working with numbers 1-19.
By first grade, students extend the counting sequence to 120, understand place value, and use this understanding to add and subtract.
Second grade students are expected to demonstrate the same skills, but they are expected to be more fluent with mental math and with three-digit numbers.
Common Core Math Examples - Number and Operations in Base 10 Sample Question
At the third grade level, students should use place value understanding and properties of operations to perform multi-digit arithmetic.
This includes the ability to round numbers, fluently add and subtract within 1000 using an understanding of place value, and multiply one-digit whole numbers by multiples of 10.
Fourth grade students should be able to generalize place value understanding for multi-digit whole numbers. For example, a fourth grade students should recognize that a digit in one place represents ten times what it represents in the place to its right.
They are also expected to use place value understanding to perform multi-digit arithmetic.
For fifth grade students, understanding the place value system is expected. This includes being able to explain patterns in the placement of the decimal point when a decimal is multiplied or divided by a power of 10.
Additionally, fifth grade students should be able to perform operations with multi-digit whole numbers and decimals to the hundredths.
Number and Operations- Fractions (3-5)
Fractions are introduced in third grade, at which point students should begin to understand fractions as numbers. They should also be able to represent fractions on a number line diagram and compare fractions by reasoning about their size.
Fourth grade students are expected to extend this understanding of fraction equivalence and ordering. They are also expected to build fractions for unit fractions, understand decimal notation for fractions, and compare decimal fractions. They should be able to interpret charts and graphs related to fractions.
Common Core Math Examples - Fractions Sample Question
By fifth grade, students should be able to use equivalent fractions as a strategy to add and subtract fractions and apply and extend their previous understanding of division and multiplication. For example, they should understand that fractions represent the division of the numerator by the denominator.
Measurement and Data (K-5)
In kindergarten, students are asked to describe and compare measurable attributes, such as weight and length. They are also expected to classify objects and count the number of objects in each category.
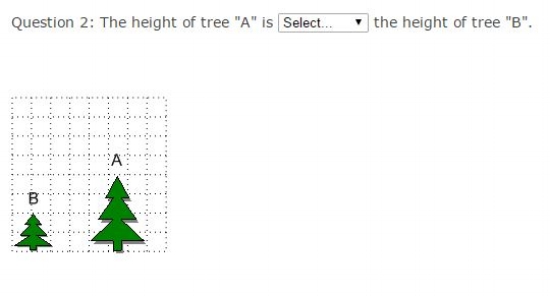
First grade students must measure items indirectly, such as comparing the length of two items using a third object. They should also tell and write time and represent and interpret data.
Common Core Math Examples -Measurement and Data Sample question
Second grade students should be able to:
By third grade, students will be solving problems involving measurement and estimation. They should also understand area and recognize perimeter.
Fourth grade students should measure angles and understand concepts of angles and solve problems involving measurements and conversion of measurements.
Lastly, fifth grade students are meant to convert like measurement units and understand concepts related to volume.
Common Core Math Examples - Measurement and Data Sample 2
Geometry (K-12)
Geometry is introduced in kindergarten, at which point students should identify, describe, analyze, compare, and create shapes.
Students in grades 1-3 are expected to reason and with shapes and their attributes, with this understanding expanding each year.
Fourth grade students are asked to draw and identify lines and angles. They must also classify shapes based on properties of their lines and angles.
Fifth grade students should graph items on a coordinate plane and use this information to solve real world problems, and they should be able to classify two dimensional figures based on their properties.
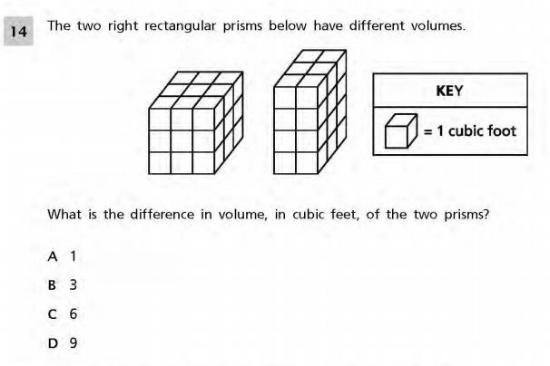
Sixth grade students are required to solve real-world and mathematical problems related to area, surface area, and volume.
Common Core Math Examples - Geometry Sample Question
By seventh grade, students should know how to draw, construct, and describe geometric figures and the relationship between them. They should also be able to solve both real world and mathematical problems pertaining to area, surface area, volume, and angle measure.
Eighth grade students are asked to:
High school students must additionally demonstrate understanding of congruence, circles, trigonometry, modeling with geometry, and geometric proportions.
Common Core Math Examples -Geometry Sample Question 2
Ratios and Proportional Relationships (6-7)
Starting in sixth grade, students should be able to use ratios and ratio reasoning to solve mathematical and real world problems.
By seventh grade, students should be able to do the same by analyzing and understanding proportions and proportional relationships.
Common Core Math Examples - Ratios and Proportions Sample Question
In sixth grade, students are expected to divide fractions by fractions, find factors and multiples of multi-digit numbers, and begin understanding the system of rational numbers.
At the seventh grade level, students should apply and understanding their previous knowledge of fractions. This includes multiplying and dividing rational numbers.
Eighth grade students should understand that there are numbers that are not rational, and approximate them by rational numbers.
For example, they should be able to use rational approximations of irrational numbers in order to compare them in size.
In sixth grade, students are asked to extend their previous understanding of arithmetic to algebraic expressions, solve one-variable equations and inequalities, and analyze relationships between independent and dependent variables.
Seventh grade students are expected to use properties of operations to generate equivalent expressions. They are also asked to solve real world and mathematical problems using algebraic expressions and equations.
Lastly, eighth grade students should be able to work with radicals and integer exponents and solve pairs of simultaneous linear equations.
Common Core Math Examples - Equations and Expressions
In sixth grade, students should begin to develop an understanding of statistical variability. They should also be able to summarize and describe distributions, including median and mean.
Seventh grade students are expected to use random sampling to draw inferences about a population, draw informal comparative inferences about two populations, and develop, use, and evaluate probability models.
By eighth grade, students should be able to investigate patterns of association in bivariate data. This includes constructing and interpreting scatter plots.
High school students are expected to:
Common Core Math Examples - Statistics and Probability
Functions (8-12)
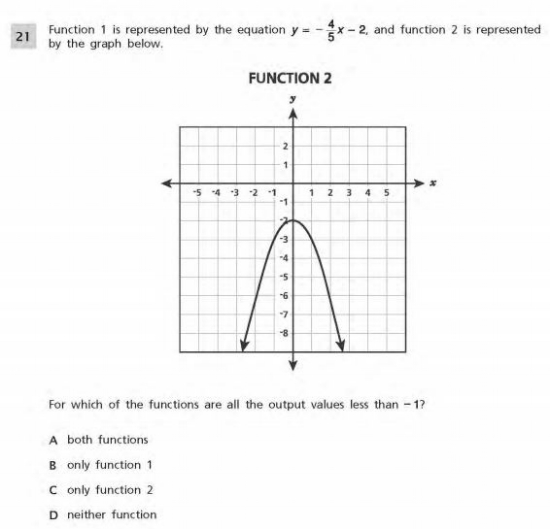
Beginning in eighth grade, students should define, evaluate, and compare functions. They should also be able to use functions to model relationships between quantities.
Common Core Math Examples -Functions
High school students must interpret and build functions, including linear, quadratic, and exponential models and trigonometric functions.
High school students must additionally demonstrate an extended understanding of algebra, modeling, and complex quantities including vectors and matrices.
Will My Child Take a State Test on Common Core Math?
It depends. Following the implementation of Common Core, the Department of Education awarded funds to two consortiums to develop standardized assessments aligned with Common Core.
These consortiums are the Partnership for the Assessment of Readiness for College and Career (PARCC) and the Smarter Balanced Assessment Consortium (SBAC).
PARCC is made up of the following states:
SBAC member states include:
Even if you are not in one of these states, the standardized math test your child will be asked to take will likely include many concepts based on or similar to the ideas of Common Core math.
We hope that the explanations and Common Core math examples in this article have helped you feel more knowledgeable and comfortable with Common Core mathematics!